Kuinka löytää rinnakkaismuodon terävä kulma?

Rinnamogrammi on nelikulmio, jossa vastakkaiset sivut ovat pareittain rinnakkaisia.

Ristikudoksella on kaikki nelikulmioiden ominaisuudet, mutta sillä on myös omat ominaisuutensa. Tietäen heidät, löydämme helposti rinnakkaismuodon molemmat sivut ja kulmat.

Parallelogram Properties

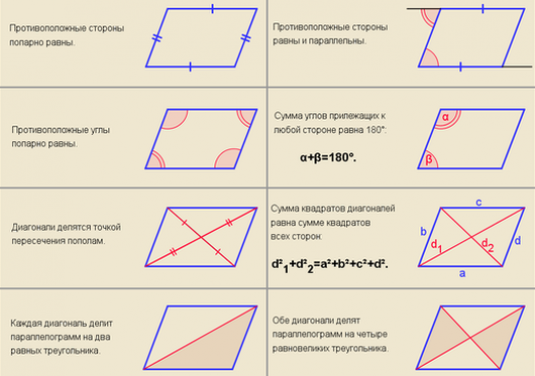
1. Minkä tahansa rinnakkaismallin kulmien summa, kuten missä tahansa nelikulmassa, on 360 °.
2. Rinnakummun keskilinjat ja sen lävistäjä leikkaavat yhdestä pisteestä ja jakavat sen puoliksi. Tätä kohtaa kutsutaan yleensä parallelogrammin symmetrian keskukseksi.
3. Vastakohdan vastakkaiset sivut ovat aina yhtä suuret.
4. Myös tässä kuvassa on aina vastakkaiset kulmat.
5. Kellojen summa, jotka ovat vierekkäin rinnakkaismuodossa, ovat aina 180 °.
6. Samansuuntaisen kuvion diagonaalien neliöiden summa on kaksi kertaa sen kahden vierekkäisen sivun neliöiden summa. Tämä ilmaistaan ​​kaavalla:
   • d₁² + d₂² = 2 (a²+ b²), jossa d₁ ja d₂ - diagonaalit, a ja b - vierekkäiset sivut.
7. Tiheän kulman kosini on aina alle nolla.

Miten löydetään tietyn parallelogrammin kulmat,näiden ominaisuuksien soveltaminen käytännössä? Ja mitkä muut kaavat voivat auttaa meitä tässä? Tarkastellaan tiettyjä tehtäviä, jotka edellyttävät: etsiä parallelogrammin kulmat.

Rinnakkaismuodon kulmien löytäminen

Tapaus 1. Tiheän kulman mittaus tunnetaan, sen on löydettävä terävä kulma.

Esimerkki: Ristikudoksessa ABCD kulma A on 120 °. Etsi muiden kulmien mitta.

ratkaisu: Ominaisuuden nro 5 avulla voimme löytää kulman B mittauksen ongelman kulman vieressä. Se on yhtä suuri kuin: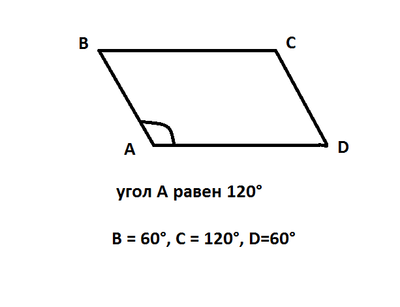

• 180 ° -120 ° = 60 °

Ja nyt, käyttämällä kiinteistön numeroa 4,että kaksi jäljellä olevaa kulmaa C ja D ovat vastakkaisia ​​kuin ne, jotka olemme jo löytäneet. Kulma C on kulmaa A vastapäätä, kulma D kulmalle B. Siksi ne ovat pareittain yhtä suuret kuin ne.

• Vastaus: B = 60 °, C = 120 °, D = 60 °

Tapaus 2. Sivut ja lävistäjät ovat tiedossa

Tällöin on käytettävä cosine-lause.

Voimme ensin laskea tarvittavan kulman kosinin kaavasta ja sitten selvittää erityisestä taulukosta, mitä kulma itsessään on.

Akkukulman osalta kaava on:

• cosa = (А² + ² - d²) / (2 * А * В), missä
• a on haluttu akuutti kulma,
• A ja B ovat parallelogrammin puolia,
• d - pienempi lävistäjä

Tuttu kulma kaava muuttuu hieman:

• cosß = (А² + В² - D²) / (2 * А * В), missä
• ß on tylppä kulma,
• A ja B ovat sivuja,
• D - suuri lävistäjä

Esimerkki: on välttämätöntä löytää rinnakkaismuodon terävä kulma, jonka sivut ovat 6 cm ja 3 cm ja pienempi lävistäjä on 5,2 cm

Korvaa kaavan mukaiset arvot etsimään akuuttia kulmaa:

• cosa = (6² + 3² - 5.2²) / (2 * 6 * 3) = (36 + 9 - 27,04) / (2 x 18) = 17,96 / 36 ~ 18/36 ~ 1/2
• cosa = 1/2. Pöydän mukaan saadaan selville, että vaadittu kulma on 60 °.
• Vastaus: 60 °