Miten löytää kehä ja alue?

Mielenkiintoista, monta vuotta sitten tällainen osamatematiikkaa, "geometriaa" kutsuttiin "maatutkimukseksi". Ja miten löytää kehä ja alue, se tunnetaan jo pitkään. He sanovat esimerkiksi, että näiden kahden määrän ensimmäiset laskimet ovat Egyptin kansaa. Tällaisen tiedon ansiosta he voisivat rakentaa nykyään tunnettuja rakennuksia.
Kyky löytää alue ja kehä voihyödyllistä jokapäiväisessä elämässä. Arkielämässä näitä arvoja käytetään silloin, kun on tarpeen maalata, istuttaa tai käsitellä puutarha, tapetit huoneeseen jne.
kehä
Useimmiten on tarpeen selvittää kehämonikulmioita tai kolmioita. Tämän arvon määrittämiseksi on vain tarpeen tietää kaikkien sivujen pituudet, ja kehä on niiden summa. Etsi kehä, jos alue tunnetaan, on myös mahdollista.
kolmio
Jos sinun täytyy tietää kolmion ympärys,sen laskemiseksi on tarpeen soveltaa sellaista kaavaa P = a + b + c, jossa a, b, c ovat kolmion sivut. Tällöin tavallisen kolmion kaikki sivut tasossa summataan.
kierros
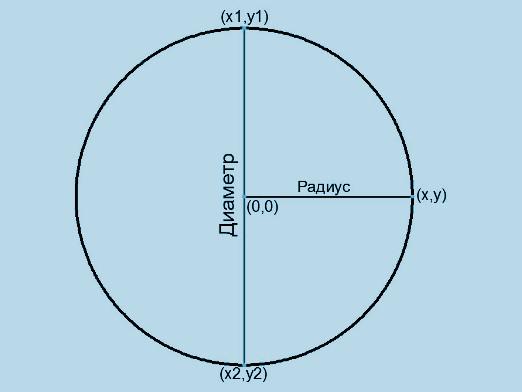
Ympyrän kehää kutsutaan yleensä pituudeksiympyrä. Tämän arvon selvittämiseksi on käytettävä kaavaa: L = π * D = 2 * π * r, missä L on kehä, r on säde, D on halkaisija ja numero π tunnetaan olevan noin 3,14.
Neliö, timantti
Kaava neliön ja timantin kehälleovat samat, koska sekä yksi luku että muut kaikki sivut ovat yhtä suuret. Koska neliöllä ja rombolla on yhtäläiset sivut, niiden (sivut) voidaan merkitä yhdellä kirjaimella "a". Näyttää siltä, että neliön ja timantin ympärysmitta on yhtä suuri kuin:
- P = a + a + a + a tai P = 4a
Suorakulmio, parallelogramm
Suorakulmion ja rinnakkaismuodon tapauksessa vastakkaiset sivut ovat samat, joten ne voidaan merkitä kahdella eri kirjaimella "a" ja "b". Kaava näyttää tältä:
- P = a + b + a + b = 2a + 2b. Kahdesta voidaan päätellä sulkeista ja saadaan seuraava kaava: P = 2 (a + b)
trapetsi
Trapezilla kaikki sivut ovat erilaisia, joten niitä kutsutaan latinalaisin kirjaimilla. Tässä suhteessa puolisuunnikkaan kehän kaava näyttää:
- P = a + b + c + d Tässä kaikki sivut summataan yhteen.
Lisätietoja kehän laskemisesta on kohdassa Miten löytää kehä.
alue
Alue - sen osan muoto, joka on suljettu sen ääriviivoon.
suorakulmio
Jokaisen suorakaiteen alueen laskemiseksi,on tarpeen moninkertaistaa toisen puolen arvo (pituus) toisen (leveyden) arvon avulla. Jos pituus- ja leveysarvot on merkitty kirjaimilla "a" ja "b", alue lasketaan kaavalla:
- S = a * b
neliö
Kuten jo tiedetään, neliön sivut ovat yhtä suuret, joten alueen laskemiseksi voit yksinkertaisesti ottaa yhden sivun neliöön:
- S = a * a = a2
vinoneliö
Mummopinta-alueen kaavaan on hieman erilainen muoto: S = a * hamissä ha on timantti, joka piti puolella korkeus pituus.
Lisäksi alueen vinoneliö tunnistaa kaavat:
- S = a2* sin α, on puoli muoto ja kulma the kulman α osapuolten välillä;
- S = 4r2/Sin α, jossa ovat on säde kirjoitettu diamond ympyrä ja kulma α on osapuolen välinen kulma.
kierros
Ympyrän alue on myös helppoa. Tällöin voit käyttää kaavaa:
- S = ΠR2missä R on säde.
trapetsi
Jos haluat laskea alueen puolisuunnikas, voit käyttää tätä kaavaa:
- S = 1/2 * * b * h, missä a, b-base Puolisuunnikas, h on korkeus.
kolmio
Löytää alueen kolmion käyttää useissa kaavoissa:
- S = 1/2 * (a) * b sin α (jos a, b-puolia kolmion ja α-kulma niiden välillä);
- S = * 1/2 h (jossa pohjana on kolmio, h-korkeus hänelle pois);
- S = abc/4R (a, b c-side kolmio ja R on circumradius säde);
- S = p * r (p on semiperimeter, r on säde kaiverrettu ympyrä);
- S = √ (p * (p-a p-b) (p-c)) (p on semiperimeter, a, b, c-side kolmio).
Suunnikas
Jos haluat laskea tämä muoto neliö korvaa arvot kaavoissa:
- S = * b * sin α (jos suunnikas, b-base, α on osapuolten välinen kulma);
- S = a * ha (Jos puoli suunnikas ha suunnikas, joka laski puoli korkeus);
- S = 1/2 * d * D * sin α (d ja D ollessa lävistäjä suunnikas α on kulma niiden välillä).