Kuinka ratkaista nopeusongelma?

Nopeus, aika ja matka ajon aikanaS = v * t, missä v on liikkeen nopeus, t on siirretty aika, ja S on liikkeen aloitus- ja loppupisteiden välinen etäisyys. Lisätietoja tämän magnitudin peruskorrelaatiosta on artikkelissa "Miten ratkaista liikkeen ongelma?". Alla kerrotaan, kuinka voit löytää nopeuden, etäisyyden tai ajan tehtävän.
Nopeusongelman ratkaiseminen
Esimerkkejä samanlaisista ongelmista on jo käsitelty artikkelissa Miten löytää nopeuden ja ajomatkan. Ymmärrämme algoritmin ongelmien ratkaisemiseksi nopeudella ja muilla liikkeen ominaisuuksilla.
Miten ratkaista ongelmat: perussäännöt
- Ensinnäkin meidän on otettava huomioon, että nopeusLiike tällaisissa ongelmissa on vakio: ei ole hidastumista eikä kiihdytystä. Siksi sanotaan usein vain nopeus, vaan keskimääräinen nopeus, joka on yhtä suuri kuin v = S / t.
- On tärkeää lukea tehtävä huolellisesti ja kirjoittaase matemaattisessa muodossa, i.e. poista kaikki tarpeettomat. Yhtälöt eivät välitä, kyseessä on Pete, juna tai vene, mitä he tekivät ja miksi. Tärkeintä on liike, aika, tie, nopeus. Se on kaikki ja täytyy kirjoittaa.
- Liikkumisongelman ratkaiseminen on välttämätöntäTee piirros, joka näyttää koko tien, etäisyyden, kokouspaikan jne. Sitten liikkeen luonne muuttuu välittömästi, ja on selvää, mitä tehdä tällä.
- On mahdotonta käyttää sekä metriä ettäkilometrejä, sekuntia ja tuntia. Kaikilla määrillä on oltava sama ulottuvuus. Jos ongelma kertoo, että yksi kohde oli tiellä 10 tuntia ja toinen puoli päivää, sinun täytyy kääntää se tunteina.
Esimerkki nopeusongelman ratkaisemisesta
Harkitse ongelma. Etäisyys kaupungista kylään on 45 km. Jalankulkija tuli kaupunkiin nopeudella 5 km / h kylästä. Tunnin kuluttua pyöräilija, jonka nopeus oli 15 km / h, tapasi tavata hänet kaupungista kylään. Kumpi heistä on lähempänä kylää kokouksen ajankohtana?
Luemme huolellisesti ja kirjoitamme ongelman olosuhteet:
- S = 45 km
- v1 = 5 km / h.
- v2 = 15 km / h.
- t1 - t2 = 1 h - jalankulkija jätti tuntia aikaisemmin, sitten ennen kokousta pidempään.
- s1 =? s2 =? - Sen selvittämiseksi, kuka oli lähempänä kylää, on tiedettävä molempien polku.
Teemme piirustuksen. Piirrämme viivasegmentin, jonka loppuun merkitään Village (C) ja City (D).
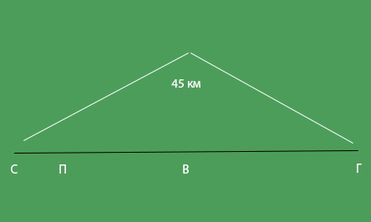
Piirrosta voidaan nähdä, että:
- S = s1 + s2, 45 = s1 + s2 (1).
Reitin kaavalla
- s1 = t1 * v1 = 5 * t1 (2)
- ja s2 = t2 * v2 = 15 * t2 (3).
Ongelman olosuhteista
- t1 - 1 = t2 (4).
Korvataan (4) osaksi (3):
- s2 = 15 * (t1 - 1) (5).
Nyt korvataan (2) ja (5) perusjaksollamme (1):
- 45 = 5 * t1 + 15 * (t1 - 1) (6)
Jakamalla molempien puolien yhtälö 5:
- 9 = t1 + 3 * t1 - 3.
Yhtälön vasemmalla puolella on -3:
- 12 = 4 * t1, saavutamme
- t1 = 3 tuntia.
Kolme tuntia jalankulkija matkustaa 15 km, joten pyöräilijä kulkee 30. Hän on lähempänä kylää.