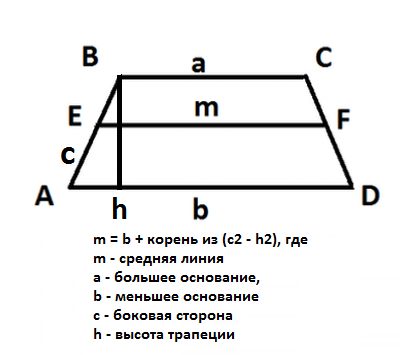
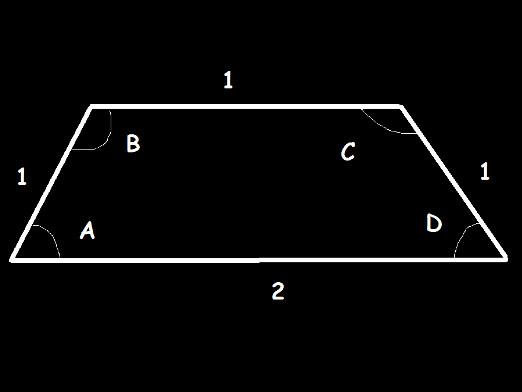
Miten löytää trapetsin korkeus?

Trapetsia on nelikulmio, kaksijonka sivut ovat yhdensuuntaisia (nämä ovat trapetsin pohjat, jotka on merkitty kuvioissa a ja b), ja kaksi muuta eivät ole (kuvassa AD ja CB). Trapetsin korkeus on segmentti h, joka on kohtisuorassa pohjaan nähden.
Kuinka löytää trapetsin korkeus tunnetuille puolivälialueille ja pohjan pituuksille?

Laskettaessa puolisuunnikkaan ABCD-alueen S käytämme kaavaa:
S = ((a + b) × h) / 2.
Tällöin segmentit a ja b ovat trapetsin pohjat, h on trajektin korkeus.
Tämän kaavan muuntamisen avulla voimme kirjoittaa:
h = 2 × S / (a + b)
Käyttämällä tätä kaavaa saadaan h: n arvo, jos alueen S ja emästen a ja b pituudet tunnetaan.
esimerkki
Jos tiedetään, että puoliperäosan S pinta-ala on 50 cm², pohjan a pituus on 4 cm, pohjan b pituus on 6 cm ja korkeuden h löytämiseksi käytämme kaavaa:
h = 2 × S / (a + b);
Vaihdamme tunnetut määrät kaavaan.
h = (2 × 50) / (4 + 6) = 100/10 = 10 cm
Vastaus: Trapetsin korkeus on 10 cm.
Kuinka löydän trapetsin korkeuden, jos puolisuunnikkaan alue ja keskilinjan pituus annetaan?

Käytämme kaavaa laskettaessa trapetsoidun alueen:
S = m × h,
Tässä m on keskilinja, h on trajektin korkeus.
Jos kysytään, miten löytää trapetsin korkeus, kaava:
h = S / m, on vastaus.
Täten löydämme trapezin h korkeuden, jolla on tunnetut aluealueen S arvot ja keskiviivan m segmentti.
esimerkki
Tunnetaan trapezin m keskilinjan pituus, joka on 20 cm ja alue S, joka on 200 cm2. Löysääksemme puolisuunnikkaan h korkeuden arvon.
h = S / m.
S: n ja m: n arvojen korvaaminen:
h = 200/20 = 10 cm
Vastaus: Trapetsin korkeus on 10 cm
Miten löytää suorakulmaisen trapetsin korkeus?

Jos puolisuunnikas on nelikulmio, jossa on kaksirinnanpuoliset sivut (pohjat). Diagonaali on segmentti, joka yhdistää trapetsikulmien kaksi vastakkaista kärkiä (kuvion segmentti AC). Jos puolisuunnikas on suorakaiteen muotoinen, diagonaalisesti käytetän puolisuunnikkaan h.
Suorakulmainen trapetsia on puolisuunnikas siten, että yksi sivuista on kohtisuorassa pohjaan nähden. Tässä tapauksessa sen pituus (AD) on sama kuin korkeus h.
Katsokaa siis suorakaiteen muotoista puolisuunnatusta ABCD: stä,jossa AD on korkeus, DC on pohja, AC on lävistäjä. Käytämme Pythagoraan lauseita. Suorakulmion kolmion ADC hypotenuse AC: n neliö on yhtä suuri kuin sen jalkojen AB ja BC neliöiden summa.
Sitten voimme kirjoittaa:
AC² = AD² + DC².
AD on kolmion katetri, puolisuora puolisuunnikkaan ja samalla korkeus. Loppujen lopuksi AD-segmentti on kohtisuorassa pohjaan nähden. Sen pituus on:
AD = √ (AC² - DC²)
Joten, meillä on kaava laskettaessa korkeus trapetsia h = AD
esimerkki
Jos pituus suorakulmainen pohja puolisuunnikkaan (DC), joka on 14 cm, ja lävistäjä (AC) on 15 cm ja korkeus arvo (AD -bokovoy puoli) käyttää Pythagoraan lausetta.
Olkoon x oikean kolmion (AD) tuntematon jalka sitten
AC² = AD² + DC² voidaan tallentaa
15 ² = 14 ² + ²²,
х = √ (15²-14²) = √ (225-196) = √29 cm
Vastaus: suorakulmaisen puolisuunnikkaan (AB) korkeus on √29 cm, joka on noin 5,385 cm
Miten löydän isosceles trapetsin korkeuden?

Isosceles trapetsia kutsutaan trapetsiksi, ySivupuolen pituudet ovat yhtä suuret kuin toiset. Tällaisen puolisuunnikkaan tukipohjien keskikohdan läpi vetävän suoran viiva on symmetrian akseli. Erityinen tapaus on puolisuunnikas, jonka lävistäjät ovat kohtisuorassa toisiaan vasten, korkeus h on yhtä kuin puolet peruspalkkojen summasta.
Tarkastellaan tapausta, jos diagonaalit eivät oleovat kohtisuorassa toisiinsa nähden. Tasapainotteisissa (isosceles) puolisuunnikossa kulmien läpimitat ja pituudet ovat yhtä suuret. On myös tiedossa, että kaikki tasasivupuolen puolipisteiden kärjet koskettavat trapetsiä ympäröivän ympyrän viivaa.
Harkitse piirustusta. ABCD on isosceles trapezoid. On tunnettua, että pohjan suuntainen puolisuunnikkaan avulla, BC = b rinnan AD = a, sivu AB = CD = c, niin, kulmiin emäkset vastaavasti, voidaan kirjoittaa kulma BAQ = CDS = α, ja kulma ABC = BCD = β. Siksi päätämme, että kolmio ABQ on yhtä suuri kuin kolmio SCD, joten segmentti
AQ = SD = (AD-BC) / 2 = (a-b) / 2.
Sillä edellytyksellä, että ongelma ja emäksen arvo b, ja sivun pituus s, huomaamme, puolisuunnikkaan korkeus h on yhtä suuri kuin segmentin BQ.
Harkitse oikea kolmio ABQ. BO on trapeziumin korkeus, joka on kohtisuorassa alustaan AD, ja siten segmenttiin AQ. ABQ: n kolmiomme AQ, löydämme, käytämme kaavaa, jonka olemme aiemmin saaneet:
AQ = (a - b) / 2.
Oikean kolmion kahden jalan arvojen avulla löydämme hypotenuse BQ = h. Käytämme Pythagoraan lauseita.
AB² = AQ² + BQ²
Korvaa tehtävätiedot:
c² = AQ² + h².
Saamme kaavan löytää isosceles trapezoidin korkeus:
h = √ (c2-AQ2).
esimerkki
Kun kyseessä on isosceles trapezoid ABCD, jossa pohjaAD = a = 10 cm, pohja BC = b = 4 cm ja sivu AB = c = 12 cm. Tällaisissa olosuhteissa harkitsemme esimerkiksi, kuinka löytää trapetsikorvaus, ABCD: n isosceles trapezoidi.
Löydämme ABQ: n kolmion sivun AQ korvaamalla tunnetut tiedot:
AQ = (a-b) / 2 = (10-4) / 2 = 3 cm.
Korvaa nyt kolmion sivujen arvot Pythagoraanin lauseessa.
h = √ (c²-AQ²) = √ (12² - 3 ²) = √135 = 11,6 cm.
Vastaa. Isosceles trapezoid ABCD: n korkeus h on 11,6 cm.