Miten löytää keskimmäinen trapetsinen linja?

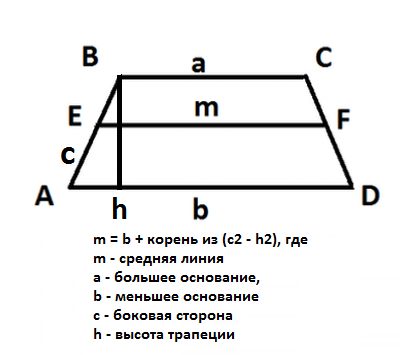
Sivusuunnan keskiosaa yhdistävä suora viivapuoliväliä, kutsutaan trapetsin keskiviivaksi. Miten löytää keskimmäinen trapezium-linja ja miten se liittyy muihin tämän kuvion osiin, keskustelemme jäljempänä.
Keskitason lause
Piirrä trapetsia, jossa AD on suurempibase, BC - pienempi pohja, EF - keskilinja. Jatketaan D-pisteen peruspistettä. Piirrä linja BF ja jatka sitä, kunnes se leikkaa pohjan AD jatkamisen pisteessä O. Harkitse kolmioita ΔBCF ja ΔDFO. Kulmat ∟BCF = ΔDF pystysuoraan. CF = DF, ∟BCF = ΔFDO, koska ВС // АО. Tällöin kolmiot ΔBCF = ΔDFO. Siten sivut BF = FO.

Katso nyt ΔABO ja ΔEBF. ∟ ABO on yleinen molemmille kolmioille. BE / AB = ½ tila, BF / BO = ½, koska ΔBCF = ΔDFO. Näin ollen kolmio ABO ja EFB ovat samankaltaisia. Siten sivujen EF / AO = ½ suhteellinen suhde sekä muiden osapuolten suhde.
Löydämme EF = ½ AO. Piirustuksesta voidaan nähdä, että AO = AD + DO. DO = BC tasaisten kolmioiden sivuina, siis AO = AD + BC. Tällöin EF = ½ AO = ½ (AD + BC). eli Trapetsin keskilinjan pituus on puolet perusmäärän summasta.
Onko trapetsin keskiviiva aina yhtä suuri kuin puolet perusmääristä?
Oletetaan, että on olemassa erityinen tapaus,kun EF ≠ 1 (AD + BC). Sitten BC ≠ DO, siis ΔBCF ≠ ΔDCF. Mutta tämä on mahdotonta, koska niillä on kaksi samanlaista kulmaa ja sivuja niiden välillä. Näin ollen teorema on tosi kaikissa olosuhteissa.
Keskitason ongelma
Oletetaan, että meidän trapetsin ABCD AD / BC, ∟ A = 90 °, ∟ C = 135 °, AB = 2 cm, diagonaalinen AC on kohtisuorassa sivusuunnassa. Etsi keskimmäinen trapetsinen linja EF.
Jos ∟ A = 90 °, niin ∟ B = 90 °, niin ΔABC on suorakulmainen.
∟ BCA = ∟ BCD - ∟ ACD. ∟ ACD = 90 ° tila, siis ∟BCA = ∟BCD - ΔACD = 135 ° - 90 ° = 45 °.

Jos suorakaiteen muotoinen kolmio ΔABC yksi kulma on 45 °, sen jalat ovat yhtä suuret: AB = BC = 2 cm.
Hypotenuus AC = √ (А²² + ВС²) = √8 cm.
Harkitse ACAC. ∟ ACD = 90 ° edellytys. ∟CAD = ∟BCA = 45 °, kun kulmat muodostivat trapeziumin secant-rinnakkaisperustat. Näin ollen jalat AC = CD = √8.
Hypotenuse AD = √ (AC² + CD²) = √ (8 + 8) = √16 = 4 cm.
Keskimääräinen trapetsiverkko on EF = ½ (AD + BC) = ½ (2 + 4) = 3 cm.