Oikean kolmion ominaisuudet

Suorakulmainen kolmio on geometrinen kuva, jossa yksi kulma on välttämättä suoraviiva. Oikealla kulmalla oleva kolmio on useita ominaisuuksia.

Perusominaisuudet

Joten oikean kolmion ominaisuudet ovat:

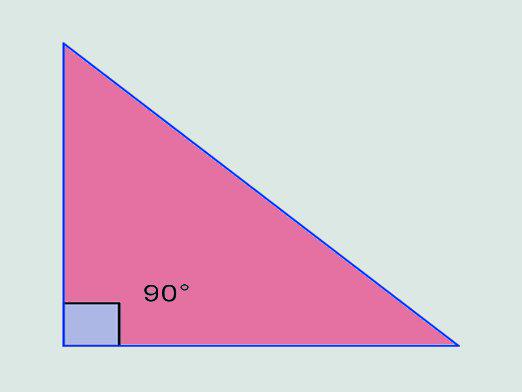
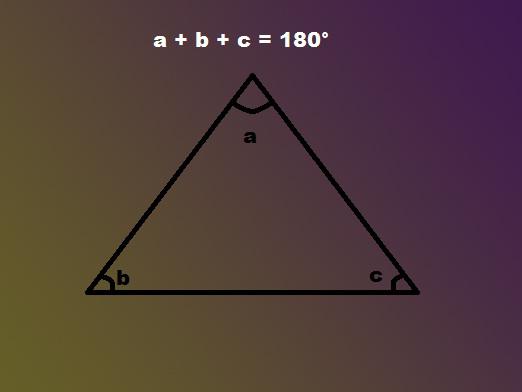
Ensimmäinen ja tärkein asia on oikea kulma, kiitosjonka hän sai nimensä. Kuten tiedät, se on 90 astetta. Summan kahden muun kulman pitäisi myös olla tämä arvo. Niinpä kuvassa kaikkien kulmien summan tulisi olla 180 astetta - tämä on oikean kolmion kulmien ominaisuus.

Toinen tärkeä ominaisuus ovat osapuoletsuorakaiteen kolmio: hypotenuus ja kaksi jalkaa. Oikean kolmion katetri, joka on 30 asteen kulmaa vastaava, on puolet hypotenusista.

Pythagoralainen teoreema

Oikeanpuoleisen kolmion ominaisuudet ovat Pythagoraanin lause: hypotenusen neliö on yhtä kuin jalkojen neliöiden voima.

C² = a² + b², missä a ja b ovat jalat, ja c on hypotenuus.

Oikean kulmaisen kolmion pinta-ala on puolet sen jaloista: S = 1 / 2ab

Median ominaisuudet

On myös huomattava, että median ominaisuuksia on oikeassa kulmassa kolmio. Hypotenuseeseen kuuluvat medianit ovat puolet.

Jos piirrämme korkeus oikealta kolmio, joka on 90^noin hypotenuteen, niin kolmio on jaettu kahteensama suorakulmainen kolmio. Tästä voimme päätellä, että suorakulmaisen kolmion korkeus on hypotenuksen kahden segmentin geometrinen keskiarvo. Näin ollen kukin katetri on keskimäärin suhteessa hypotenuteen ja vierekkäisiin segmentteihin. Sinun on myös tiedettävä, että hypotenuteen laskettava korkeus liittyy jalkoihin suhteessa: 1 / a² + 1 / b² = 1 / f² , missä a ja b ovat jalkoja, ja f on korkeus.