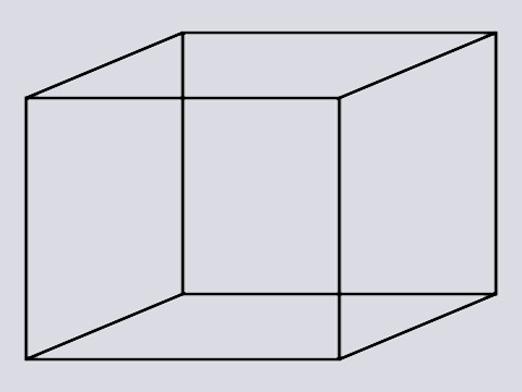
Kuinka löytää kuution pinta-ala?

Kuutio on neliön kolmiulotteinen versio. Kun tunnetaan kuution (a) reunan pituus, voidaan käyttää yleistä kaavaa pinta-alan (S) määrittämiseksi. Perustuu siihen, että neliön pinta-ala, joka vastaa pituutta neliömäisen reunan, ja on kuusi kuutio saadaan: S = 6 ∙ a². Tämä kaava määrittää kokonaispinta-ala kuution.

Menetelmät kuution alueen määrittämiseksi

1. Jos tilan tilavuus (V) on annettu, jonka reunat reunustavat kuution ja reunan pituus tuntematon, niin alue (S) määritellään tällä tavalla.

   Kun ainoa tunnettu kuvakoko,on kolmannen reunan kohoidun reunan pituus, minkä jälkeen kuution kunkin puoleisen sivun pituusmitta on määritetty poistamalla kuutunjuuri olemassa olevasta parametrista. Kuution pinta-alan kaava on: S = 6 ∙ (√√V) ².

2. Kun heksahedronin (L) diagonaalinen pituus on annettu, niinyhden kasvon pituus voidaan helposti laskea, ja yhdessä sen kanssa kuvion pinta-ala. Diagonaali määritellään seuraavasti: L / v3. Siten kuution alue lasketaan seuraavasti: S = 6 ∙ (L / √3) ² = 2 ∙ L², mikä on erittäin kätevää laskujen kannalta.
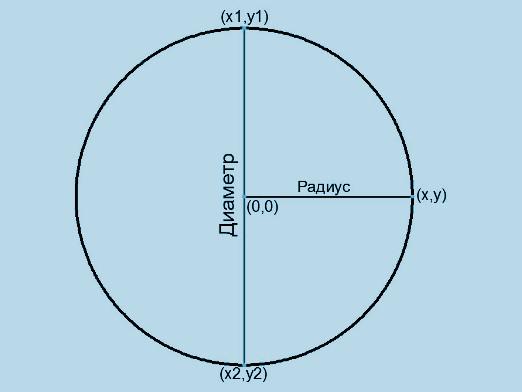
3. Kuinka löytää kuution pinta-ala määritettäessäympyrän (R) säde, jota kuvataan heksaedron ympärillä? Helppoa! Sovelletaan vain kaavaa: S = 8 ∙ R² = 2 ∙ (2 ∙ R) ². Tämä on mahdollista siksi, että kuution diagonaali vastaa palloa halkaisijan parametria.
4. Tunnetaan heksahedriin merkitty ympyrän säde, kuution pinta-alan kaava on kirjoitettu seuraavasti: S = 24 ∙ r².

Kuution pinta-ala

S = s1 + s2 + s3 + s4, jossa termit edustavat vastaavasti neljä parallelogrammia, jotka muodostavat parallelepipedin sivupinnan.

Kuution sivupinnan pinta-alan kaava voidaan esittää S = P • h, edellyttäen, että annetaan suora suuntaissärmiö, jonka pohjan P tunnetulla kehällä ja korkeudella h.

Kun laskelmat on tehtävä suorakaiteen muotoisiksisuuntaissärmiön (kaikki sen kasvot - suorakulmioita) kanssa tunnettujen pituudet puolin pohjan (d ja c), kun molemmat k - reuna-luku, kun taas lateraalinen pinta kuution määritellään seuraavasti: S = 2 • k • (d + c).