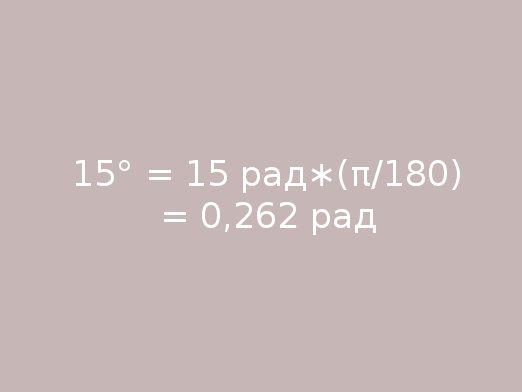Miten löytää viereinen kulma?

Matematiikka on vanhin tarkka tiede, jokapakollinen opiskelu kouluissa, korkeakouluissa, laitoksissa ja yliopistoissa. Perusosaaminen on kuitenkin aina asetettu kouluun. Joskus lapselle kysytään melko vaikea tehtävä, ja vanhemmat eivät voi auttaa, koska he vain unohtivat joitakin asioita matematiikasta. Esimerkiksi kuinka vierekkäinen kulma löytyy peruskulman arvosta ja niin edelleen. Tehtävä on yksinkertainen, mutta se voi aiheuttaa vaikeuksia ratkaista, koska tietämättömyys siitä, mitä kulmia kutsutaan vierekkäin ja miten löytää ne.

Tarkastellaan tarkemmin vierekkäisten kulmien määrittelyä ja ominaisuuksia sekä niiden laskemista ongelman tiedoista.

Viereisten kulmien määrittely ja ominaisuudet

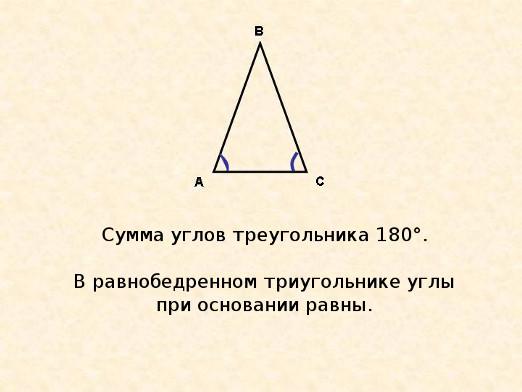
Kaksi säteilyä, jotka ovat peräisin yhdestä pisteestäkuvassa "tasakulma". Tätä kohtaa kutsutaan kulmakohdaksi, ja säteet ovat sen sivuja. Jos jatkamme yhtä säteestä aloituspisteen yli pitkin suoraa linjaa, muodostuu toinen kulma, jota kutsutaan vierekkäiseksi. Kussakin kulmassa tässä tapauksessa on kaksi vierekkäistä kulmaa, koska kulman sivut ovat vastaavia. Eli on viereinen 180 asteen kulma.

Viereisten kulmien perusominaisuudet ovat

• Vierekkäisten kulmien yhteinen kärki ja toinen puoli;
• Viereisten kulmien summa on aina 180 astetta tai numero Pi, jos laskenta suoritetaan radiaaneissa;
• Viereisten kulmien viivästeet ovat aina yhtä suuret;
• Viereisten kulmien cosines ja tangentit ovat samat, mutta niillä on vastakkaiset merkit.

Näiden ominaisuuksien vuoksi on helppo laskea viereinen kulma tietäen tietyt tiedot.

Miten löytää vierekkäiset kulmat

Yleensä kolme vierekkäisten kulmien arvon löytämiseen liittyviä ongelmia on annettu

• Peruskulman arvo annetaan;
• Pää- ja vierekkäisen kulman suhde annetaan;
• Pystysuuntaisen kulman arvo annetaan.

Jokaisella ongelman versiolla on oma ratkaisu. Harkitse niitä.

Peruskulman arvo

Jos tehtävä määrittää peruskulman arvon, niinviereisen kulman löytäminen on hyvin yksinkertaista. Tällöin riittää pienentää peruskulman arvo 180 astetta ja saat viereisen kulman arvon. Tämä ratkaisu perustuu viereisen kulman ominaisuuteen - vierekkäisten kulmien summa on aina 180 astetta.

Jos kuitenkin peruskulman arvo annetaan radiaaneissa jatarvitaan löytää tehtävän viereisen kulman radiaaneina, sitten vähennetään Pi perus- kulma-arvo, koska täyden asteikon arvo on 180 asteen kulmassa on yhtä suuri määrä Pi.

Ottaen huomioon pää- ja vierekkäisen kulman suhde

Ongelmassa pää- ja vierekkäisen kulman suhde voidaan antaa asteen sijaan ja peruskulman arvon radiaanit. Tässä tapauksessa ratkaisu näyttää suhteellisen yhtälön:

1. Me tarkoitetaan pääkulman osuuden osuutta muuttujan "Y" suhteen.
2. Merkitään vierekkäiseen kulmaan liittyvä murto muuttujaksi "X".
3. Kunkin osan suhteen laskettujen tutkintojen määrä tarkoittaa esimerkiksi "a".
4. Yleinen kaava näyttää tältä: a * X + a * Y = 180 tai * (X + Y) = 180.
5. Yhtälön "a" yhteinen tekijä on kaava a = 180 / (X + Y).
6. Sitten yhteisen tekijän "a" saatu arvo kerrotaan määritettävän kulman murto-osalla.

Siten voimme löytää viereisen arvonkulma asteina. Kuitenkin, jos haluat löytää arvon radiaaneissa, sinun on vain muutettava asteita radiaaneiksi. Tätä varten moninkertaista kulma asteina numero Pi ja jaa kaikki 180 astetta. Tulokseksi saatu arvo on radiaaneja.

Pystysuoran kulman arvo

Jos tehtävä ei anna peruskulman arvoa vaan antaa pystykulman arvon, laske viereinen kulma samalla kaavalla kuin ensimmäisessä kappaleessa, jossa peruskulman arvo on annettu.

Pystysuuntainen kulma on kulma, joka tuleeSama kohta kuin tärkein, mutta se suunnataan tarkalle vastakkaiseen suuntaan. Tämä tuottaa peilikuvan. Tämä tarkoittaa, että pystysuora kulma on yhtä suuri kuin pääkulma. Pystysuoran kulman viereinen kulma puolestaan ​​on yhtä suuri kuin peruskulman viereinen kulma. Tästä johtuen on mahdollista laskea peruskulman viereinen kulma. Voit tehdä tämän yksinkertaisesti vähentää 180 astetta pystysuoran arvon ja saada pääkulman viereisen kulman arvo asteina.

Jos arvo kuitenkin annetaan radiaaneissa, on tarpeen vähentää numerosta Pi vertikaalisen kulman arvo, koska 180 asteen kokonaisulottumattoman kulman arvo on yhtä suuri kuin lukumäärä Pi.

Myös voit lukea hyödyllisiä artikkeleita. Mikä on kulma ja mitkä ovat kulmat.