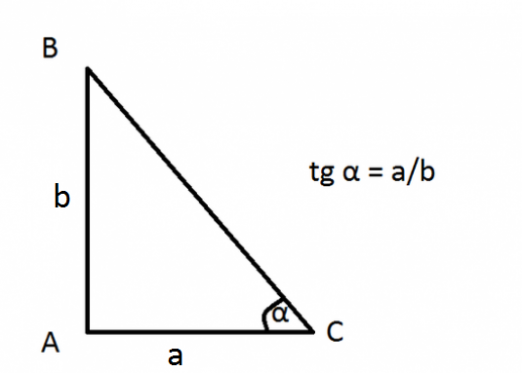
Miten löytää kulman astetta?

Katso video


Monille kouluissa geometria on todellinen asia.testi. Yksi perus geometrisista kuvista on kulma. Tällä käsitteellä tarkoitamme kahta säteilyä, jotka ovat peräisin yhdestä pisteestä. Kulman arvon (suuruuden) mittaamiseksi käytetään asteita tai radiaaneja. Miten löytää kulman astetta, opit artikkelistamme.
Tyypit kulmat
Sanotaan, että meillä on kulma. Jos hajotetaan se suoraksi linjaksi, sen arvo on 180 astetta. Tällaista kulmaa kutsutaan taittumattomaksi ja kolmasosa pitää 1/180 sen osana.
Kehittyneen kulman lisäksi on myös teräviä(alle 90 astetta), tylppä (yli 90 astetta) ja suorat (90 astetta) kulmat. Näitä termejä käytetään määrittämään asteen kulmamittauksen suuruus.
Kulmamittaus
Kulman arvo mitataan mittapinnalla. Tämä on erityinen laite, joka on puoliympyrän jaettu 180 osaa. Liittää astelevyä kulmaan siten, että toisella puolella kulman samaan aikaan alaosan astelevyn. Toisen säteen on ylitettävä kaaren astelevyn. Jos ei, poista astelevyn ja hallitsija laajentaa säteen. Jos kulma "avaa" oikealle huiput, luettu arvo ylemmän mittakaavassa, jos vasemmalle - alempi.
SI-järjestelmässä on tavallista mitata kulma sisäänradiaaneja, ei asteina. Käytetyssä kulmassa on vain 3,14 radiaania, joten tämä arvo on hankalaa ja käytännössä ei käytetä käytännössä. Siksi sinun on tiedettävä, miten kääntävät radiaanit asteiksi. Tätä varten on olemassa kaava:
- Asteet = radiaanit / π × 180
Esimerkiksi kulma on 1,6 radiaania. Tulostamme asteiksi: 1,6 / 3,14 * 180 = 92
Kulmaominaisuudet
Nyt tiedät, kuinka mitata ja laskea uudelleen kulma-asteen mittaukset. Mutta ongelmien ratkaisemiseksi on tarpeen tietää kulmien ominaisuudet. Tähän mennessä on muotoiltu seuraavat aksiomit:
- Kaikki kulmat voidaan ilmaista asteina, jotka ovat pienempiä kuin nolla. Käytetyn kulman määrä on 360.
- Jos kulma koostuu useista kulmista, sen aste- mitta on yhtä suuri kuin kaikkien kulmien summa.
- Tietyllä puolitasolla mistä tahansa säteestä voidaan muodostaa tietyn suuruisen kulman alle 180 astetta, ja vain yksi kulma.
- Samansuuruiset arvot ovat samat.
- Jos haluat lisätä kaksi kulmaa, meidän on lisättävä niiden arvoja.
Näiden sääntöjen ymmärtäminen ja kyky mitata kulmia ovat avain menestyksekkään geometrian tutkimiseen.