Kuinka rakentaa vektori?
Vektoria kutsutaan yleensä segmentiksi, jolla onmääritelty suunta. Sekä vektorin alussa että lopussa on kiinteä asento, jonka avulla vektorin suunta määritetään. Tarkastellaan tarkemmin vektorin rakentamista annettujen koordinaattien kanssa.
- Piirrä koordinaatisto (x, y, z) avaruudessa, merkitse yksittäiset segmentit akseleille.
- Aseta molemmille akseleille tarvittavat koordinaatit, piirrä niistä akselien kanssa yhdensuuntaiset katkoviivat ja leikkauspiste. Opi leikkauspiste, jonka täytyy yhdistää pisteviiva alkuperäineen.
- Piirrä vektori alkuperästä tuloksena olevaan pisteeseen.
- Aseta kolmannella akselilla haluamasi numero tämän pisteen kautta piirtää katkoviiva, joka on yhdensuuntainen konstruoidun vektorin kanssa.
- Lopusta vektorin tehdä esitetyn mukaisesti samansuuntainen kolmannen akselin leikkaa linjan viimeisen kohdan.
- Lopuksi yhdistää alkuperän ja tuloksena olevan pisteen.
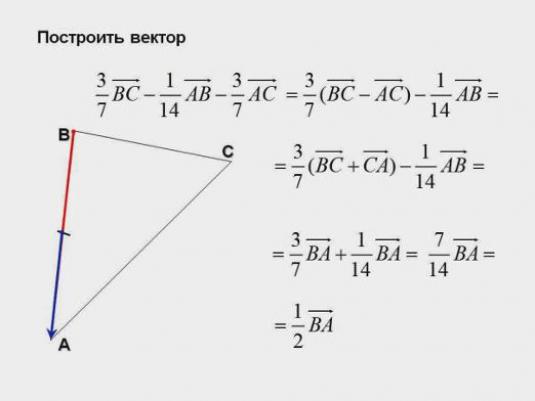
Joskus on pakko rakentaa vektori, joka on seurausta muiden vektorien lisäämisestä tai vähennyksestä. Siksi nyt harkitsemme toimintoja vektoreilla, opimme lisäämään ja vähentämään niitä.
Toiminnot vektorilla
Geometrisiä vektoreita voidaan lisätämonin tavoin. Esimerkiksi yleisin tapa vektori Lisäksi on yleisesti kolmiomainen. Lisätä kaksi vektoreita tämän säännön mukaan, on välttämätöntä järjestää vektorit yhdensuuntaisesti toisiinsa siten, että kun ensimmäinen vektori samaan aikaan toisen pään, kolmannen kolmion saadaan vektorin summa.
Voit myös laskea vektoreiden summan säännön mukaansuunnikas. Vektorien tulee alkaa yhdestä pisteestä rinnakkain kuhunkin vektoriin, joten sinun on piirrettävä viiva niin, että tuloksena oleva parallelogrammi saadaan. Rakennetun rinnakkaismuodon lävistäjä on näiden vektorien summa.
Jotta vähennetään kaksi vektoria, meidän on lisättävä ensimmäinenvektori ja vektori, joka on toisen vastakohta. Tätä tarkoitusta varten käytetään myös yleisesti kolmio, jolla on seuraava koostumus: erotusvektoreiden siirretään siten, että ne alkavat osuvat, on vektori, jonka alku yhtyy pään vähentäjä vektorin, sekä pään kanssa pelkistetyn vektorin.