Miten ratkaista moduulit?
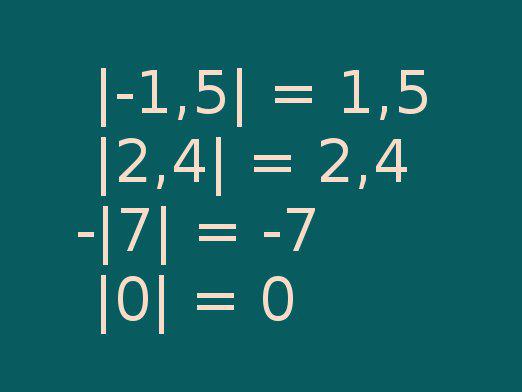
Moduuli on lausekkeen absoluuttinen arvo. Jotkin moduulin nimeäminen on tavallista käyttää suoria sulkeita. Tämä arvo, joka on suljettu samansuuruisiin suluihin, on arvo, joka otetaan moduulissa. Prosessin ratkaiseminen tahansa moduuli paljastaa samat suorat kannattimet, joita kutsutaan modulaarinen suluissa matemaattisella kielellä. Niiden julkistaminen tapahtuu tiettyjen sääntöjen mukaan. Moduulien ratkaisemisen järjestyksessä on myös joukko arvoja näistä lausekkeista, jotka olivat modulaarisissa suluissa. Useimmissa tapauksissa moduuli laajennetaan siten, että submodulaarinen ilmentymä saa sekä positiivisia että negatiivisia arvoja, mukaan lukien nolla. Jos aloitamme moduulin vakiintuneista ominaisuuksista, prosessissa käsitellään erilaisia yhtälöitä tai epätasaisuuksia alkuperäisestä lausekkeesta, jotka sitten on ratkaistava. Katsotaanpa miten moduulit ratkaistaan.
Ratkaisuprosessi
Moduulin ratkaisu alkaa alkuperäisen tallennuksen avullayhtälöt, joiden moduuli on. Jotta voit vastata kysymykseen, miten ratkaista yhtälöt moduulilla, sinun on avauduttava kokonaan. Tällaisen yhtälön ratkaisemiseksi moduuli paljastuu. Kaikki modulaariset lausekkeet on otettava huomioon. Olisi määritettävä, mitkä arvot tuntemattomista määristä muodostavat sen koostumuksen, modulaarinen lauseke suluissa muuttuu nollaksi. Tätä varten riittää, että lauseke modulaarisissa suluissa nollataan ja laske tuloksena olevan yhtälön ratkaisu. Löydetyt arvot olisi korjattava. Samalla tavalla meidän on myös määritettävä kaikkien tuntemattomien muuttujien arvo kaikille moduuleille tietyssä yhtälössä. Seuraavaksi meidän on käsiteltävä kaikkien muuttujien olemassaolon esiintymistiheyden määrittelyä ja tarkastelua silloin, kun ne poikkeavat nollasta. Tätä varten meidän on kirjattava eräitä epäyhdenvertaisuusjärjestelmiä vastaavasti kaikkiin alkuperäisen epätasa-arvon moduuleihin. Eriarvoisuudet on suunniteltava niin, että ne kattavat kaikki käytettävissä olevat ja mahdolliset arvot muuttujalle, jotka löytyvät numeroriviltä. Sitten sinun täytyy piirtää tämä erittäin numeerinen viiva visualisointiin, josta tulevaisuudessa lykätään kaikkia vastaanotettuja arvoja.
Lähes kaikki voi nyt tehdä Internetissä. Moduuli ei ole poikkeus sääntöihin. Ratkaise verkossa se voi olla yksi monista nykyaikaisista resursseista. Kaikki ne muuttujan arvot, jotka ovat zerotimoduulissa, ovat erityinen rajoitus, jota käytetään modulaarisen yhtälön ratkaisemisessa. Alkuyhtälössä vaaditaan avaamaan kaikki käytettävissä olevat moduulirakenteet, samalla kun muutetaan lausekkeen merkkiä, niin että vaaditun muuttujan arvot ovat samat kuin ne arvot, jotka näkyvät numerolinjalla. Tuloksena oleva yhtälö on ratkaistava. Yhtälön ratkaisun aikana vastaanotettavan muuttujan arvo on tarkistettava rajoittajalle, jonka moduuli itse määrittelee. Jos muuttujan arvo täyttää täysin ehton, se on oikein. Kaikki juuret, jotka saadaan yhtälön ratkaisun aikana, mutta joita ei rajoiteta rajoituksiin, on hylättävä.
Esimerkkiliuos:










