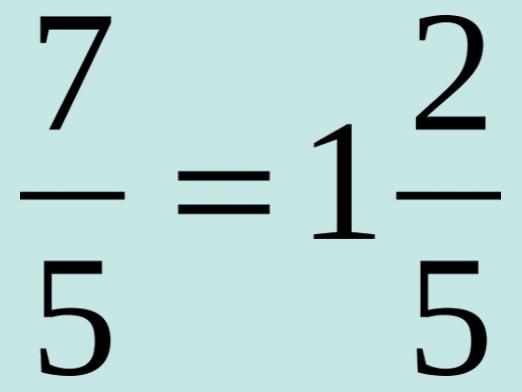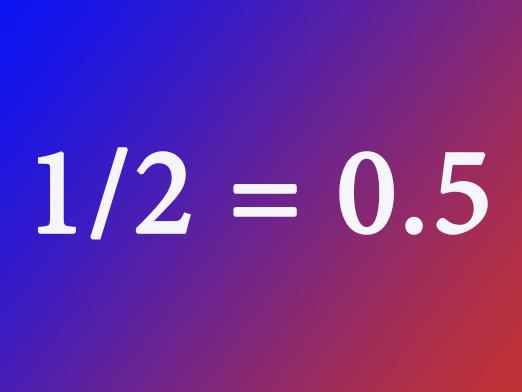Kuinka muuntaa desimaali tavalliseksi murto-osaksi?
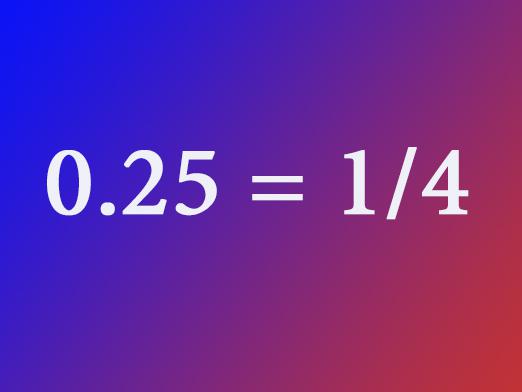
Kymmenesosuus koostuu kahdesta osasta, jotkaerotetaan pilkulla. Ensimmäinen osa - koko yksikkö, toinen osa - kymmeniä (jos numero desimaalipisteen jälkeen yksi), satoja (kaksi numeroa desimaalipisteen jälkeen, kun kaksi nolla sata), tuhansia ja niin edelleen. Katsokaamme esimerkkejä desimaalin 0, 2; 7, 54; 235,448; 5,1; 6,32; 0,5. Kaikki nämä ovat desimaaleja. Kuinka muuntaa desimaali tavalliseksi murto-osaksi?
Esimerkki yksi
Meillä on murto, esimerkiksi 0,5. Kuten edellä mainittiin, se koostuu kahdesta osasta. Ensimmäinen numero 0 osoittaa, kuinka monta kokonaista yksikköä murto-osassa. Meidän tapauksessamme he eivät ole. Toinen luku näyttää kymmeniä. Fraktio on jopa luettu nolla nolla 5 kymmenesosaa. Desimaaliluku siirto telalle nyt se ei ole vaikeaa, kirjoitamme 5/10. Jos näet, että numeroilla on yhteinen jakaja, voit lyhentää murto-osaa. Meille tämä numero 5, joka on jaettu molempien fraktion osiin 5, saamme - 1/2.
Esimerkki toisesta
Otetaan monimutkaisempi osa - 2,25. Se lukee näin - kaksi kokonaista ja kaksikymmentäviisiosasataa. Huomautus - satoja, koska desimaalipilkun jälkeiset numerot ovat kaksi. Nyt voit kääntää normaaliksi murto-osaksi. Tallennamme - 2 25/100. Koko osa on 2, murtoarvo on 25/100. Kuten ensimmäisessä esimerkissä, tätä osaa voidaan lyhentää. Numerojen 25 ja 100 yhteinen jakaja on luku 25. Huomaa, että valitsemme aina suurimman yhteisen jakajan. Jakamalla kummankin osan fraktiota GCD: llä saatiin 1/4. Joten, 2, 25 on 2 1/4.
Esimerkki kolmannesta
Ja korjaa materiaali, ota desimaaliosa 4112 - ja peräti neljäsataakaksitoista tuhannesosaa. Miksi tuhannesosa, luulen, on selvä. Tallennamme nyt 4 112/1000. Mukaan algoritmi löytää GCD numerot 112 ja 1000. Meidän tapauksessamme - se on numero 6. Get 4 14/125.
johtopäätös
- Jakimme murto-osan kokonaislukuun ja murto-osaan.
- Katso, kuinka monta desimaalia desimaalipilkun jälkeen. Jos yksi - se on kymmeniä, kaksi - satoja, kolme tuhannesosaa jne.
- Merkitsemme murto-osan tavallisessa muodossa.
- Pienennämme murto-osan numeerista ja nimittäjää.
- Talleta vastaanotettu fraktio.
- Teemme testin, jaetaan murto-osan yläosa pohjaan. Jos on olemassa kokonaislukuosa, lisää se vastaanotettuun desimaalilukuun. Tuloksena oli alkuperäinen versio - ihana, niin teit kaiken oikein.
Esimerkeissä osoitin kuinka voit muuntaa desimaalilajin tavalliseksi murto-osaksi. Kuten näette, tämä on erittäin helppoa ja yksinkertaista.