Miten löytää sini, jos kosini tunnetaan?

Kun ilmenee ongelma, jossa tiedetääntrigonometrinen funktio, ja sen on löydettävä toinen trigonometrinen funktio, sitä ei ole vaikea ratkaista. Mutta on erittäin tärkeää ottaa huomioon ratkaisun pienet subtletit. Harkitse yksityiskohtaisia ratkaisuja, kun otetaan huomioon vivahteet. On useita muunnelmia ongelmia, joissa sen on löydettävä sinia, jos kosini tunnetaan.

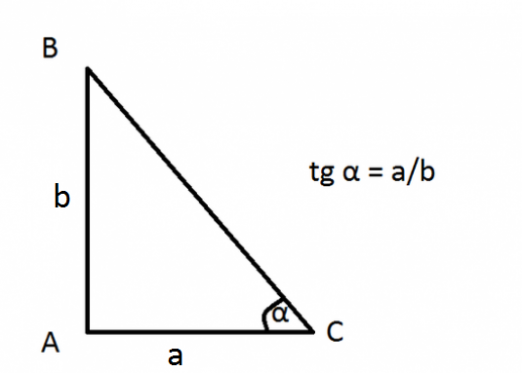
Vaihtoehto 1. Suorakulmainen kolmio annetaan. Tämän kolmion kulman (ei oikean kulman) kosini on tiedossa. Nastya on sine.

ratkaisu:

Muistuta perus trigonometrinen identiteetti: sin²α + cos ²α = 1.

Siksi synti²α = 1 - cos²α.

sin α = ± √ (1- cos²α)

Oikeassa kulmassa oleva kolmio kulman arvo (ei suora) voi olla alueella 1⁰ jopa 89⁰. Sellainen kulma on aina positiivinen, joten ennen juuria, meillä on plus.

Variantti 2. Joidenkin kulman kosini tunnetaan. Tiedetään myös, mikä kvartsi trigonometrisestä ympyrästä kulma kuuluu.

ratkaisu:

synti²α + cos ²α = 1.

synti²α = 1 - cos²α.

sin α = ± √ (1- cos²α)

Tiedetään, että trigonometrinen funktio on siniavoi ottaa arvot -1: sta +1: een. Siksi, kun poistamme juuri, meidän on otettava tämä huomioon. Riippuen siitä, mikä vuosineljännes kuuluu kulmaan, aseta merkki "+" tai "-" juurelle.

Mitkä ovat neljäsosaa:

I (ensimmäinen) - α 0⁰ jopa 90⁰;
II (toinen) - α alkaen 90⁰ jopa 180⁰;
III (kolmas) - α 180: sta⁰ jopa 270⁰;
IV (neljäs) - α 270: sta⁰jopa 360⁰.

Jos kulma kuuluu ensimmäiselle tai toiselle neljännekselle, emme laita juuria "-" ennen merkkiä, koska tässä tapauksessa sin α on aina positiivinen.

Jos kulma kuuluu kolmannelle tai neljännelle neljännekselle, niin ennen juurimerkkiä laukaisimme "-", koska tässä tapauksessa sin α on aina negatiivinen.

Esimerkki. Kun otetaan huomioon kosini, etsi sinia. cos a = v3 / 2. Kulma neljännellä neljänneksellä.

ratkaisu:

Joten, miten löytää sinia, tietäen kosini:

sin α = ± v (1- cos²α)

Koska ongelman olettamana kulma kuuluu trigonometrisen ympyrän neljänteen neljännekseen, laukaisimme merkin "-" ennen juuria.

sin α = -v (1-3 / 4)

sin α = - 1/2.

Esimerkki. Nelikulmaisessa kolmiossa yhden kulman kosini on 1/2. Etsi tämän kulman sine.

Ratkaisu: synti²α + cos ²α = 1.

synti²α = 1 - cos²α.

Koska etsimme oikean kulmaisen kolmion kulmaa, "+" -merkki juuren eteen.

sin α = v (1- cos²α)